The genetic algorithm simulates biological evolution in which organisms adapt to their environment by repeating mutation, crossover and selection for many generations. It is commonly used to find optimal solutions and applied to various problems, such as the low-air-resistance “Aero Double Wing” design of bullet trains.

The algorithm begins by initializing a population of individuals using default or random values. Then, it runs each member of that population through a fitness function. It selects the fittest members of the population to reproduce using a method defined in the reproduction function, then repeats the evaluation and reproduction until a desired number of iterations have passed. At termination, the algorithm presents the best member or members of the population according to the fitness function. Let’s discuss each of these concepts further. To explain this post we will apply a genetic algorithm that reproduces the text “hellow world”.

Table of contents:

Genetic Algorithm Basics

Each individual in the population must be represented by a value or object, which must be stored in a data structure. A basic example is each individual being a tuple of values and the population is a list of such tuples. An individual can also be an object or class, with whatever attributes and methods you implement. The population data structure may also place constraints upon the simulation, for example, the distance between two individuals in a list or two-dimensional array may be important in some functions.

  1. [Start] Generate random population of n chromosomes (suitable solutions for the problem)
  2. [Fitness] Evaluate the fitness f(x) of each chromosome x in the population
  3. [New population] Create a new population by repeating following steps until the new population is complete
    1. [Selection] Select two parent chromosomes from a population according to their fitness (the better fitness, the bigger chance to be selected)
    2. [Crossover] With a crossover probability cross over the parents to form a new offspring (children). If no crossover was performed, offspring is an exact copy of parents.
    3. [Mutation] With a mutation probability mutate new offspring at each locus (position in chromosome).
    4. [Accepting] Place new offspring in a new population
  4. [Replace] Use new generated population for a further run of algorithm
  5. [Test] If the end condition is satisfied, stop, and return the best solution in current population
  6. [Loop] Go to step 2

Fitness Function

The fitness function is the heart of a genetic algorithm. The function takes an individual and determines how well it fulfills whatever criteria the algorithm is optimizing for.

The fitness function should be applied to each individual of the population separately to determine whether they should be allowed to reproduce. The function may return a fitness score or a boolean for whether the individual passes a set threshold for reproduction.

In this case, we might define a cost function to be something like the following:

For each character in the string, figure out the difference in ASCII representation between the candidate character and the target character, and then square it so that the “cost” is always positive.

For example, if we have a capital “A” (ASCII 65) but it’s supposed to be a capital “C” (ASCII 67), then our cost for that character is 4 (67 - 65 = 2, and 2^2 = 4).

Using that rule as a cost function, we can calculate the costs of the above 5 example chromosomes (in parentheses):

  • Gekmo+ xosmd (7)
  • Gekln, worle" (5)
  • Fello, wosld (5)
  • Gello, wprld (2)
  • Hello, world (0)

Selection Function

The selection function takes the population and the results of the fitness function to determine who should reproduce. If the fitness function had a set threshold for reproduction and returned a boolean, then the selection function simply filters the population by that value. However, if the fitness function returned raw scores, the selection function calculates a threshold from those scores. For example, it may calculate the average score and only keep the top half of the population. It passes the selected population into the reproduction function and deletes the rejected individuals.

Reproduction Function

The reproduction function determines how to expand the population based on the existing members. Modifying the behavior and hyperparameters of the reproduction function is one of the most complex and impactful parts of creating a genetic algorithm, as the reproduction function is what determines how the population changes over time.

The simplest reproduction method is mutation, where each new member is based on a single individual. If you are doubling the population by mutation, for each individual create a new individual with the same characteristics modified by a random factor.

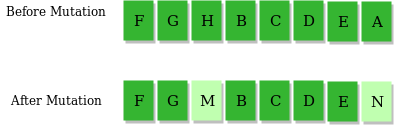
https://media.geeksforgeeks.org/wp-content/uploads/genetic-algorithm2.png

Here’s an example to illustrate. Let’s say you end up with these two chromosomes:

Hfllp, worlb

Hfllp, worlb

Your two chromosomes are exactly the same. That means that their children will be exactly the same as the parents, and no progress will ever be made. But if 1 in 100 chromosomes has one letter randomly mutated, it’s only a matter of time before chromosome #2 above turns into “Ifllp, worlb!” – and then the evolution continues because the children will finally be different from the parents once again. Mutation pushes the evolution forward.

Crossover is a more complex method of reproduction, where each new individual is based on some combination of existing individuals. Crossover still mutates the new organism’s attributes, but does so by applying a function of multiple organisms’ attributes. These two approaches can simulate asexual and sexual reproduction, respectively, and both include random factors to advance the population as a whole and model the role of chance in real-world evolution. The reproduction function returns the new population, which may be the same size or a different size than the original population.

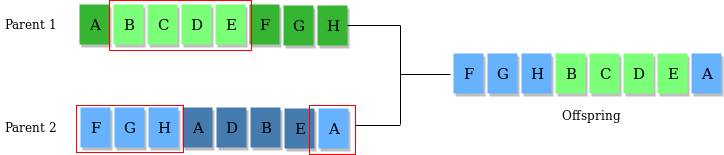
https://media.geeksforgeeks.org/wp-content/uploads/genetic-algorithm1.png

With our example, you can pick two candidates (two strings; two chromosome) and pick a point in the middle of the string. This point can be dead-center if you want, or randomized if you prefer. Take that middle point (called a “pivot” point), and make two new chromosomes by combining the first half of one with the second half of the other and vice versa. Take these two strings for example:

Hello, wprld (1)

Iello, world (1)

Cutting them in half and making two new strings from the alternating halves gives us these two new “children”:

Iello, wprld (2)

Hello, world (0)

As you can see, the offspring includes one bad child that has the worst traits of both parents, but also an good child that has the best traits of both. Mating is how you get from one generation of genes to the next.

Termination Function

After the desired iterations have occurred, the termination function takes the ending population and returns the best members by fitness score. The role of the termination function depends entirely on the application. For a video game, the termination function might output optimal statistics for the final boss, for a mathematical optimization, it returns the best input values to the function.

Now, we will consider these functions in action by implementing and evaluating a genetic algorithms.

Clone the github repository to run the example.

<
Previous Post
Prevent re-renders on React
>
Next Post
Portfolio Optimization Based on Sharpe Ratio and Genetic Algorithm